The probabilities of options trading are not so different from those in the insurance and gaming/casino industries. To make money, it helps to play the odds the way insurers and casinos do. Credit spreads are one way to do it.
One of the biggest advantages of options is the flexibility they offer. With sufficient study, you can create a strategy that meets your personal criteria for risk, reward and probability of success. Understanding and managing the relationship between these three factors is one of the most important skills option traders must master. The following discussion illustrates this by analyzing a well-known option spread.
The credit spread is an option strategy that involves selling an option while simultaneously purchasing the same type of option, with the short option being more expensive than the long option. A "vertical" credit spread indicates the options have the same expiration month.
For instance, a credit spread on stock ABC, which is trading at 16, would consist of selling the June 12.50 put (bid at 0.90) and simultaneously buying the June 10 put (offered at 0.40). The June 12.50 put is more expensive than the June 10 put, so the position provides a net credit of $0.50.
 |
The maximum profit potential for this trade is the net credit received, or $50 per spread. The maximum loss is $200 per spread, which means the risk is quadruple the potential reward. Why would anyone want to take on risk four times the maximum possible reward? The answer is probability - how frequently you get to make the $50 profit vs. how frequently you take the $200 loss. In this case, the prior historical price action of the stock indicated the probability of keeping the $50 - i.e., the strategy's winning percentage - was nearly 90 percent.
Implementing high-probability trades such as this is the opposite of what the majority of beginning traders do in the options market. When most people speculate with options (as opposed to using them to hedge a position in the underlying instrument) they tend to buy cheap options, hoping to hit a home run and make a huge profit with relatively small risk.
The credit spread strategy is a substantially different approach. It's not that buying options outright is a bad idea. But realistically, if you are simply buying them hoping to hit the jackpot, you should know your odds of winning are about equal to playing the tables at a casino. And casinos don't go out of business too often because of gambling losses.
That's because casinos (and even state lottery commissions) know and manage the risk, reward and probability of profit for the games of chance they run. It's similar to the insurance business, although the risk, reward and probability model in this area is far more complex. However, individual investors can use the same principles in the options market.
In the insurance business, you make money when something does not happen.
 |
Insurance companies collect premiums, which they get to keep if you don't get sick, you don't get into an automobile accident, your house does not catch fire, etc.
Individual traders can replicate this concept with the credit spread, essentially turning themselves into insurance companies, by selling an option, collecting a premium and keeping it as long as the stock does not move adversely.
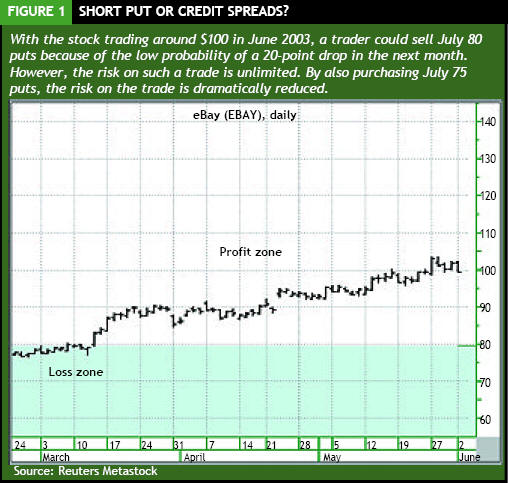
Let's look at what happens when you sell an option. Back in June 2003, prior to eBay's stock split when the price was $100, let's say you sold 20 of the eBay July 80 puts at 0.85 (see Figure 1). The net credit for the put sales was $1,700, which was the position's maximum profit. You would get to keep that credit as long as the stock was above the 80 strike price at expiration.
Based on the one-year historical volatility of the stock at the time (42 percent), the odds of the stock being below 80 at July expiration were less than 7 percent, which means there was a 93-percent chance the stock would not be below 80. In other words, the odds were great a loss would not occur.
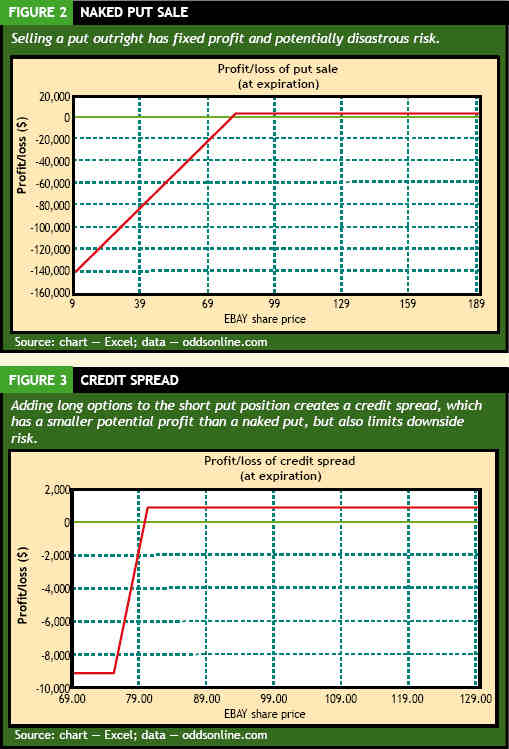
The problem is the maximum risk on this trade is $80 per share (the strike price of the put sold) multiplied by 100 (number of shares each option represents) multiplied by 20 (the number of puts old): $160,000! So while this trade has a great probability of profit, and a decent possible reward, it carries with it potentially catastrophic risk (see Figure 2).
Selling "naked," or uncovered , options in this manner has ruined more than one financial company in the past several years. The centuries-old Barings Bank is one institution that suffered the consequences of a solitary trader who sold a huge number of options in the expectation a big move would not occur in the Japanese market over a short period of time. But it did, and Barings collapsed as a result.
In effect, selling a naked option (particularly a call) is very similar to selling an insurance policy with no limit to the size of the claim. Lloyd's of London used to sell this kind of policy. Unfortunately, all it takes is one bad claim to bring catastrophe. In the case of Lloyd's, it was asbestos.
If unlimited liability is the problem, then limiting the liability is the solution. Insurance companies have two ways to do that. First, they can set a limit on the amount the policy will pay. The second solution is to buy reinsurance.
With reinsurance, the company that wrote the policy takes a portion of the premium collected from the policyholder and buys coverage for part of the policy's risk. However, this seemingly simple and effective solution has a downside: By capping the loss in this fashion, you also reduce the profit. That's the trade-off.
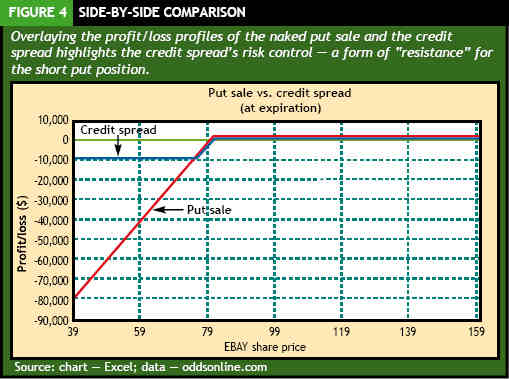 |
Traders can do the same thing with options. Returning to the eBay example, taking $800 of the $1,700 premium and buying 20 July 75 puts at 0.40 would establish a credit spread and effectively reinsure the original naked put position. The net credit (and maximum possible profit) is now $900, but the maximum risk is now much lower, as well. The long put option provides coverage for the risk that eBay would trade below $75.
The total risk on a vertical credit spread is the difference in strike prices minus the net credit. In this case, the difference in strike prices is 5. The net credit is 0.45 (0.85 - 0.40 = 0.45). Thus, the trade's maximum risk is 4.55 (5.00 - 0.45 = 4.55), or $455 per spread. With this trade consisting of 20 spreads, the total risk has dropped from $160,000 to just $9,100 (see Figure 3). To some traders these numbers still might not look very good. Comparing the put credit spread to the naked put sale, the profit potential on the spread dropped by almost half - from $1,700 to $900. And although the maximum risk is down to $9,100 - much lower than before - it's still 10 times higher than the potential reward. Figure 4 compares the naked put sale directly to the credit spread.
The key to the success of this trade is probability. The probability of any loss is less than 7 percent, and the probability of reaching the maximum loss is less than 3 percent. When you quantitatively balance these probability numbers with risk and reward, you find the trade has a positive expected outcome. (See the "Gauging probability" sidebar, below.)
The probability figures are derived from standard volatility models and the probability assumptions in the Black-Scholes option pricing formula. Basically, if a distribution of values (such as prices or price changes over a period of time) is "normal," it takes the shape of a bell curve, and one standard deviation will contain approximately two-thirds of all the values in the data set. Two standard deviations will contain 95 percent of all the numbers in the set. By definition, volatility is equal to one standard deviation of an asset's price returns. As a result, because of the implications of the bell curve, volatility produces a standard deviation, which in turn produces a probability.
The options industry doesn't like the comparison, but the analytics of options trading are not too far removed from the analytics of games of chance.
Casinos offer games that almost exclusively have expected outcomes that are positive for the casino, negative for the player. Nevertheless, for the casino operator, the risk in each incremental game is substantially larger than the rewards. With every pull of the slot machine lever, someone has the opportunity to win a jackpot. That's what keeps people coming back. If there was no jackpot, there would be no players.
The question for the casino is, how many times does someone put money in the slot machine and lose it before they hit a winning combination?
Lottery commissions depend upon games where the reward potential to the lottery board is just $1, and the potential risk could be a massive $80 million. The question is, how many of those $1 lottery tickets get sold before a player collects the $80 million jackpot?
Insurance companies depend upon people making claims for losses. After all, if there were no losses, insurance would be needless. For insurers, the questions are: How much money can we collect before we have to pay a claim? How likely is it that a claim will be filed? How big will that claim be?
In the end, the analysis is the same with options. How much can the spread trader collect? How likely is it that the trader will lose? How big will the loss be? This is the link between probability in options, re-insurance and gambling
The content of this site is copyright 2016 Financial Spread Betting Ltd. Please contact us if you wish to reproduce any of it.